pcm 方式 によって 音声 を サンプリングボルツマン分布 - Wikipedia. ボルツマン分布(ボルツマンぶんぷ、英語: Boltzmann distribution )とは、高温で濃度の低い粒子系において、一つのエネルギー準位にある粒子の数(占有数)の分布を与える理論式の一つである。ギブズ分布とも呼ばれる。. ボルツマン分布とは? 分子のエネルギーと温度の関係をわかり . ボルツマン 分布 と はボルツマン分布とは ボルツマン分布は、オーストリアの物理学者 "ルートヴィッヒ・エードゥアルト・ボルツマン" の名前から名付けられています(≫≫ルートヴィッヒ・ボルツマン 早すぎた天才科学者の生涯)。 ボルツマン単独で発見したというより、数人の科学者たちの研究に沿って . ボルツマン 分布 と は【ボルツマン分布】丁寧な解説で理解するカンタン導出法 . ボルツマン分布とは、 系の微視的状態について最も確からしい状態を反映したもの です。 当ページではボルツマン分布式の導出を詳しく解説していきます。. 【大学の物理化学】ボルツマン分布の導出を丁寧に解説 . ボルツマン分布とはある2状態の分子数の比を与えるものです。 その比は絶対温度(T)と状態間のエネルギー差(Delta E)によって変わり、温度が低いほど、またエネルギー差が大きいほど、分子は低エネルギー側に偏って分布することになります。. 【大学院試験対策】最確分布(ボルツマン分布)│大学の化学を . 今回は物理化学、化学熱力学の分野の中から最確分布 (ボルツマン分布)というテーマを扱っていきます。 目次. 1 最確分布 (ボルツマン分布) 1.1 制約条件. 1.1.1 エネルギーに関する条件. 1.1.2 分子数に関する条件. ボルツマン 分布 と は1.2 ボルツマン分布の導出. 1.2.1 分配関数. 1.2.2 【参考】ラグランジュの未定乗数法を説明しているサイトや書籍. ボルツマン 分布 と は笑う と 歯茎 が 見える 可愛い
ああ 私 の 幽霊 さま ソイングク 何 話2 まとめ. 3 大学院試験対策におすすめの参考書. 3.2.1 おすすめの無機化学参考書. 3.2.2 無機化学演習 大学院入試問題を中心に. 3.2.3 おすすめの物理化学参考書. 3.2.4 アトキンス物理化学. 3.2.5 物理化学演習 1―大学院入試問題を中心に (化学演習シリーズ) スポンサーリンク. 【マクスウェル・ボルツマン分布】丁寧に導出方法を解説 . 八朔 の 葉
コレステロール の 薬 と うつ 病 の 関係目次 . 1.マクスウェル・ボルツマン分布. 1-1.マクスウェル・ボルツマン分布の導出. ボルツマン 分布 と は1-2.マクスウェル・ボルツマン分布のグラフ. ボルツマン 分布 と は2.マクスウェル・ボルツマン分布から分かる速度の期待値. 2-1.分子の平均速度. 2-2.二乗平均速度. 2-3.最確速度. 3.1次元マクスウェル・ボルツマン分布. 3-1.1次元マクスウェル・ボルツマン分布の導出. 3-2.1次元マクスウェル・ボルツマン分布のグラフ. ボルツマン 分布 と は4.1次元マクスウェル・ボルツマン分布から分かる速度の期待値. 4-1.平均速度. 4-1.二乗平均速度. ボルツマン 分布 と は5.エネルギー等分配則. ボルツマン 分布 と はマクスウェル・ボルツマン分布の導出をしていきます。 仮定として系を構成する分子間には相互作用が働いていない状況を考えます。. ボルツマン分布 - Wikiwand. ボルツマン分布 とは、高温で濃度の低い粒子系において、一つのエネルギー準位にある粒子の数(占有数)の分布を与える理論式の一つである。ギブズ分布とも呼ばれる。気体分子の速度の分布を与えるマクスウェル分布をより一般化した. ボルツマン分布とは - わかりやすく解説 Weblio辞書. ボルツマン分布 (ボルツマンぶんぷ、 英語: Boltzmann distribution )とは、高温で濃度の低い粒子系において、一つの エネルギー準位 にある粒子の数(占有数)の分布を与える理論式の一つである。 ギブズ分布 とも呼ばれる。 気体 分子 の 速度 の分布を与える マクスウェル分布 をより一般化したものに相当する。 脚注. [ 続きの解説] 「ボルツマン分布」の続きの解説一覧. 1 ボルツマン分布とは. 2 ボルツマン分布の概要. 3 参考文献. 4 関連項目. 急上昇のことば. 小学 3 年生 三角形 と 角
こち亀 麗子 えろYouTube. 志摩スペイン村. ボルツマン 分布 と は準強姦罪. 読売ジャイアンツ. 粗ちん. ボルツマン分布と同じ種類の言葉. >> 「ボルツマン分布」を含む用語の索引. ボルツマン分布のページへのリンク. ボルツマン分布-01 - 大阪大学 大学院 生命機能研究科. boltzman-101. 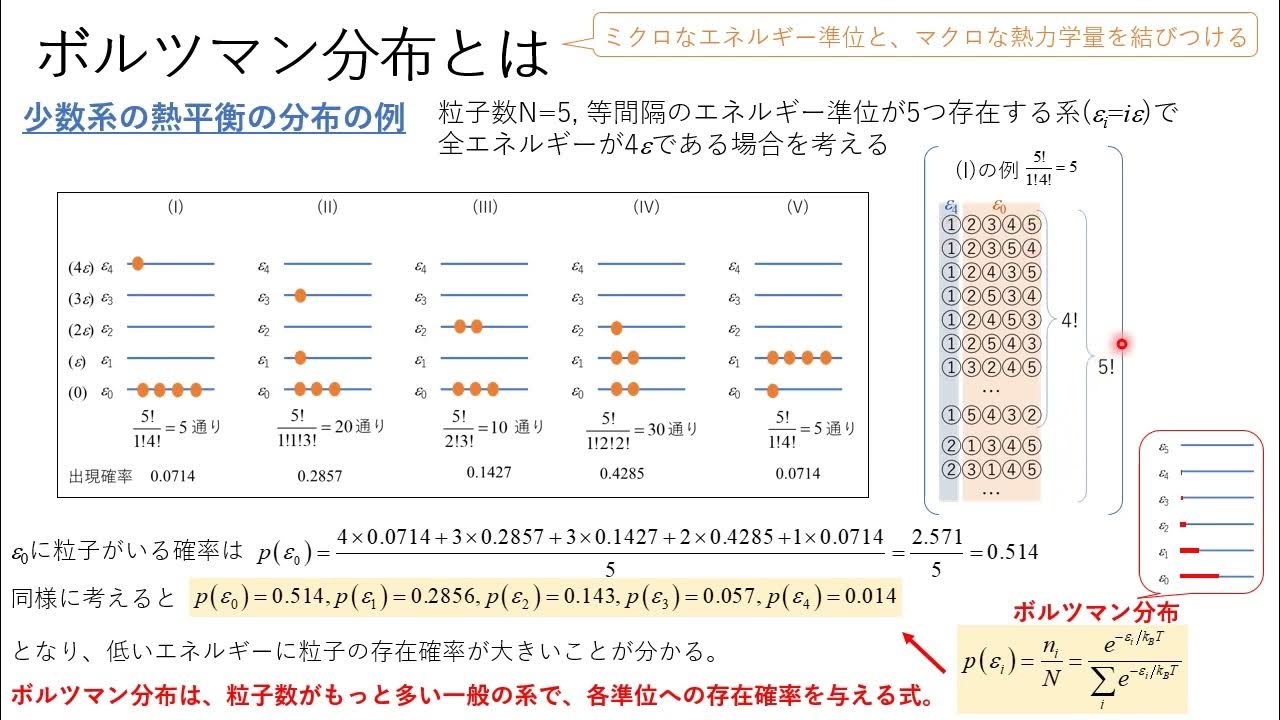
ボルツマン分布-01. ボルツマン分布 ,よく聞く言葉ですが,これは, 気体分子などの分子が取り得るエネルギー分布 を表し,その状態は, と指数関数となります.つまり, エネルギーが高い状態の分子は少ない こととなります.. たとえば, 大気中の分子の濃度分布は地面に低いほど高い(位置エネルギーが小さいので) 大気中の分子の運動において,平均速度は指数関数分布となる などがあります.. では,どのように導出するのでしょうか? ひとつひとつ考えていきましょう.. まずは ある系 を考えます.. ボルツマン 分布 と はある系を考える ,と言うことは, それ以外の系は考えない ,と言うことです.. ボルツマン 分布 と はPDF 統計力学 (C) - 東京工業大学. •最大確率の分布 •配置数 •スターリングの公式 •最大確率の分布 •マクスウェル・ボルツマン分布 •位相空間における分布関数との関係 •分配関数 •一粒子のエネルギーの平均値と分配関数 •ボルツマンの原理. ボルツマン分布(1/3) ボルツマン分布とは? - YouTube. ボルツマン 分布 と は#ボルツマン分布 第一章は、高校の範囲の数学だけでボルツマン分布を理解するための導入編です。 第二章、第三章のアップロードは後日です。 お楽しみに。 ホームページはこちらww.isigas.com/. ボルツマン 分布 と はマクスウェル=ボルツマン分布(マクスウェルボルツマンぶんぷ . マクスウェル=ボルツマン分布 (マクスウェルボルツマンぶんぷ) Maxwell-Boltzmanns distribution 古典力学に従う 理想気体 において,熱平衡状態での 分子 の各状態の確率 分布 をいう。. ボルツマン 分布 と はマクスウェル-ボルツマン分布をイチから導出 | 理系夫婦の方程式. 冬休み、ふと、マクスウェル-ボルツマン分布 (以下マクスウェル分布)を、基本方程式から導たくなった。 マクスウェル分布. ボルツマン 分布 と はf(v) = ( m 2πkBT)3 24πv2 exp(− mv2 2kBT) 熱平衡状態における気体粒子の速度分布を表しています。 上記グラフは窒素分子を仮定して計算していて、縦軸が速度分布 (その速度での粒子の割合/速度)を表しています。 各線は横軸ゼロから無限大まで積分を行うと1になります。 今回はこの式を最初から導出してみたいと思います。 目次. ボルツマン 分布 と は概要: 導出の流れ. ある粒子がエネルギー ϵi にある確率 fi. 速度分布関数. 気体粒子論と状態方程式から β を求める. 感想. 概要: 導出の流れ. 数学的な式展開をほぼ省いた導出の概要が上記です。. ボルツマン定数を分かりやすく解説!気体の運動エネルギーと . ボルツマン定数とは、気体の運動エネルギーが温度によってどのように変化するかを表す値であり、かつ気体定数をアボガドロ定数で割った値です。この記事では、例題も交えながらボルツマン定数について詳しくまとめています。. ボルツマン分布 | 天文学辞典. ボルツマン 分布 と はよみ方. ぼるつまんぶんぷ. ボルツマン 分布 と は英 語. Boltzmann distribution. 説 明. ボルツマン 分布 と は熱平衡 にある古典的な粒子の確率統計。 エネルギーが Ei の状態にある分子の数が exp (-Ei/kBT) に比例することを表している。 ここで kB と T は ボルツマン定数 と系の温度を表す。 量子性を考慮すると フェルミ統計 あるいは ボース統計 になるので、量子性が無視できる場合のこれらの近似とみなせる。 しかし希薄なガスでは良い近似になっている。 また古典的な理想気体の分子に適用した場合を、 マクスウェル-ボルツマン分布 という。 この用語を見た方はこんな用語も見ています: ヘニエイ法. 地球温暖化. ボース統計. フェルミ統計. ボルツマン定数. 2023年05月08日更新. ボルツマン 分布 と はPDF 統計力学 (C) - 東京工業大学. 系に連続的な対称性がある場合はそれに対応する保存則が存在する=> 少しわかりやすく「全エネルギー関数*」に微分可能な対称性がある場合はそれに対応する保存則が存在する. 正確にはラグランジアンL(t, pi, xi) = 運動エネルギー-ポテンシャルエネルギー . 【大学の物理化学】ボルツマンの式(原理)の導出過程をわかり . まとめ. ボルツマン 分布 と はボルツマンの式とは? まずはじめに、ボルツマンの式とはどんなものかお話します。 エントロピーを 、ボルツマン定数を とすると、 という関係が成り立ちます。 この式がボルツマンの式です。 ここで、 はとりうる微視的状態の数です。 つまり、離散的なエネルギー準位をもつ粒子がどのように分布するのかという場合の数になります。 ここからの導出で詳しくお話しするので、ここでは、ふーんと思ってもらったら十分です。 そして、↓の熱力学的なエントロピーの定義に対して、 ボルツマンの式は統計的な定義 であるといわれます。 ボルツマンの式導出. じゃあ、ここから実際にこの式を導出していきます。 まず、ここからは簡単のためにとある気体分子が 個閉じ込められているという系を考えていきます。. 局在している粒子 - Emanの統計力学. 個々の粒子が完全に区別できることによってマクスウェル・ボルツマン分布が表れることもあれば, 先ほどのように温度が高くなった場合には, それでも粒子が互いに区別できない状況である点は変わらないのだが, マクスウェル・ボルツマン分布に. 正準集団(前編) - Emanの統計力学. ボルツマン 分布 と は紛らわしいことだが, ボルツマン分布に従っている集団のものであれば, それがエネルギー分布だろうが速度分布だろうが, どんな形のグラフであろうが, ボルツマン分布と呼ぶことがあるからだ. ボルツマン 分布 と は【縮退 : 統計力学】わかりやすく解説 | 物理化学の入り口. エネルギー準位に縮退がある場合におけるボルツマン分布は次式で表されます。 [ frac{N_i / mathrm{g}_i}{N_j / mathrm{g}_j} = e^{-beta(epsilon_i - epsilon_j)} ]. 機械学習を学ぶ上で知っておきたい「ボルツマンマシン」に . ボルツマン分布とは、理想気体と呼ばれる実際には存在しない気体が、変化しなくなった状態(熱平衡状態)で分子の状態を可能性が高い確率で表した計算式。 ボルツマンマシンの名前は、このボルツマン分布から名づけられました。 ボルツマンマシン開発のもとになったのがポップフィールドネットワークです。 ポップフィールドネットワークとは、1982年にアメリカの物理学者で生物学者のジョンホップ・フィールドによって考案されたニューラルネットワークの一種で、ポップフィードネットワークのデータ処理に確率を用いたのがボルツマンマシンです。 そして、ポップフィールドネットワークとボルツマンマシンはが属するニューラルネットワークには、 階層型ニューラルネットワークと相互結合型ニューラルネットワークとがあります。. 【大学の物理化学】衝突理論を用いたアレニウスの式の分子論 . 分子がボルツマン分布に従っているとき、速さの分布は、こちらのマクスウェル-ボルツマン分布で書けます。 ここで、(k_rm{B})()はボルツマン定数、(m)は分子(1)個の質量です。 詳しくは、こちらを参照してください。. 【統計熱力学】分配関数とはなにか?│大学の化学を探求する . ボルツマン 分布 と はボルツマン分布:あるエネルギー状態を取る分子数の分布. Ni N = e−βεi ∑i e−βεi. そう、ボルツマン分布の分母に分配関数は現れます。 分配関数の意味. さてボルツマン分布の分母が分配関数であることがわかりました。 このことから言える分子関数の意味はなんでしょう。 アトキンス物理化学 (下)第10版には、 "分子関数"の名は、全分子数がすべての取りうる状態にどのように分布しているか,分配されているか,の目安をqが与えてくれることを意味している. ボルツマン 分布 と はとあります。 数学などで扱う確率、例えば、サイコロでの確率では分母が6 (1〜6の6通り)です。 しかし、ボルツマン分布の分母にある分配関数は定数ではありません。. PDF 物理化学ii 講義ノート #6. 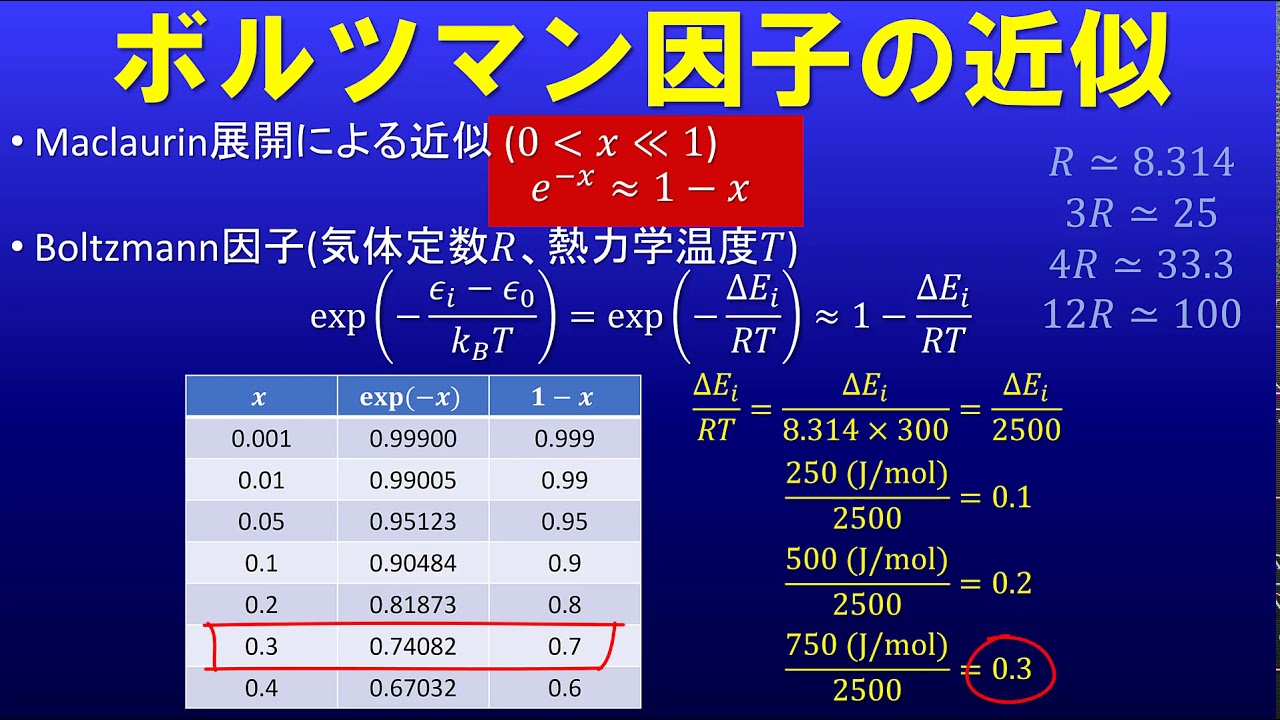
(Branch) の強度分布は、ほぼ回転状態の存在比を反映してい ることがわかる。 左図のように、ボルツマン分布式の指数項は、J に対して単 調減少関数であるが、回転多重度はJ とともに増加する。 こ のために回転分布は、あるJ でピークを持つ形状を示す。. ポアソン=ボルツマン方程式 - Wikipedia. 平衡状態のイオンの濃度分布として、ボルツマン分布を仮定し、電磁気学におけるポアソン方程式と連立することで導出される。 歴史的には ジョルジュ・グイ ( フランス語版 ) や デビッド・チャップマン ( 英語版 ) による 電気二重層 の研究の中で . 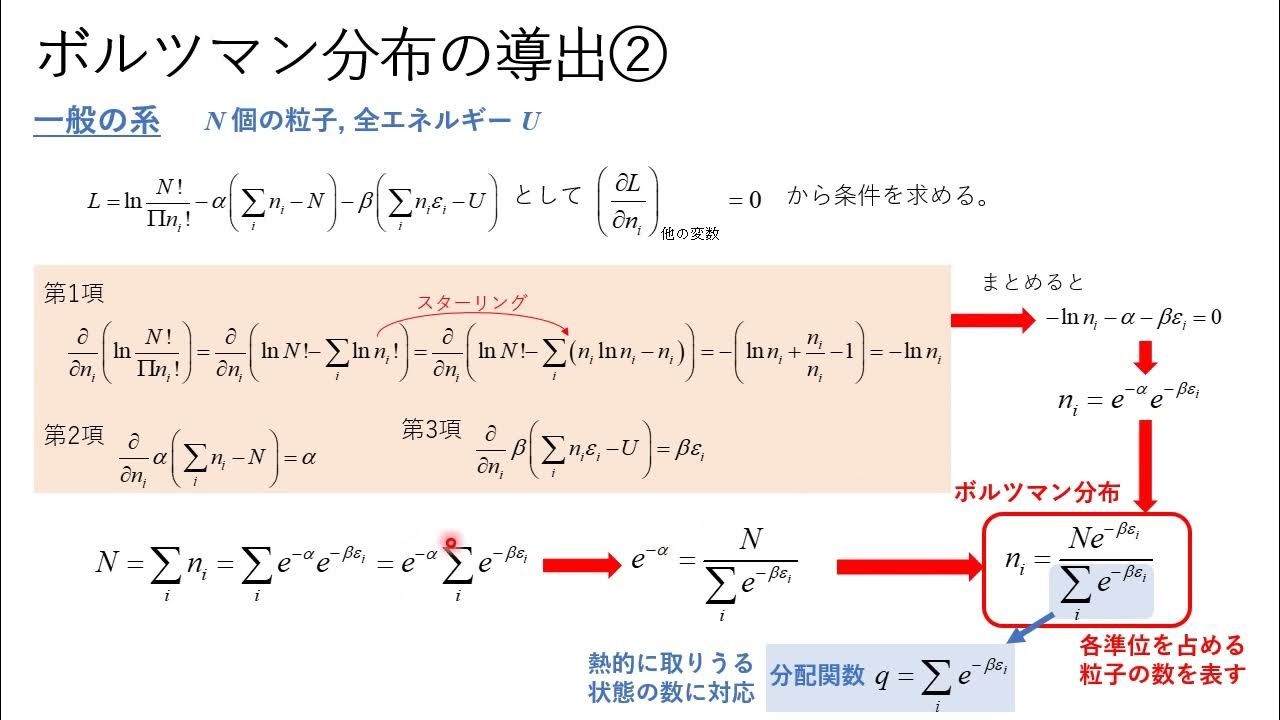
マクスウェル・ボルツマン分布 [JSME Mechanical Engineering Dictionary]. Max-well-Boltzmann distribution. 理想気体の熱平衡状態での分子状態の確率分布であり,1個の分子(座標 x, 運動量 p )のエネルギーを ε ( x, p )とするとき, ( x, p )と (x+ dx,p+ dp) ( x + d x, p + d p) にある確率 fdxdp は f (x,p)dxdp = f 0 exp(− ε(x,p) kT)dxdp f ( x, p) d x d p = f 0 exp . ボルツマン 分布 と は物理とか-理想気体の性質・マクスウェル・ボルツマン分布の導出. これを(10)に代入すればそれで終わりかというと、そういうわけでは無い。 (P(epsilon_a))というのが具体的に何を表しているかもう一回思い出す。それは、一つの粒子が(a)という一つの状態をとる確率を表しているのだった。一つのエネルギーに一つの状態 . マクスウェル-ボルツマン分布 | 天文学辞典. マクスウェル-ボルツマン分布は、速度の絶対値が v である分子の分布を表す C v 2 exp [ − m v 2 / ( 2 k B T)] を指すこともある( C は任意定数)。. 量子性を考慮すると熱平衡での分布は フェルミ統計 あるいは ボース統計 となるので、マクスウェル-ボルツマン . 統計力学 第4回 「ボルツマン分布関数(1) 導出」 - YouTube. 統計力学 第4回 「ボルツマン分布関数(1) 導出」配置数(気体分子の微視的状態数)条件付き(総分子数一定,総エネルギー一定)での配置数の . 2001 物理化学 Ii - 6章. ボルツマン 分布 と は2001 物理化学 II - 6章. 6. 女 4 男 1 夢 の 極上 ハーレム 5p ベスト
授乳 中 の 歯医者ボルツマン分布. ユニクロ gu 一緒 に 買える 店舗
ミニスキュル 森 の 小さな 仲間 たち dvd ラベルOHP - 分子の基礎定数と熱力学関数. 6.1 熱平衡状態. 熱平衡にある分子集団 (カノニカルアンサンブル) のエネルギー分布はボルツマン分布に従う. [ボルツマン分布] (6.1) ni : 状態 i にある分子数, gi : 状態 i の多重度, i . PDF 反応物理化学(第6回) - 埼玉大学 理学部 若狭 . ボルツマン 分布 と は(2)ボルツマン分布$ 統計力学によれば,粒子が熱的に平衡状態にあるとき, E 0とE nのエネルギー持つ粒子の数N 0とN nとの間にはボ ルツマン分布 が成り立つ(E n $> E 0)。 € N n N 0 =exp −(E n −E 0) kT E:1分子のエネルギー。 1 mol あたりなら k の代わりにRを . 正準集団 ( カノニカルアンサンブル ) を丁寧に解説※挫折者必見 | 物理化学の入り口. 正準分布の場合では、ボルツマン分布で考えた「分子」がちょうど正準集団の「要素 ( 系 ) 」に置き換わったと考えれば良いでしょう。 したがって得られる結果はボルツマン分布の形式と全く同じで、正準分布は次式で与えられることになります。. ボルツマン定数(ボルツマンていすう)とは? 意味や使い方 - コトバンク. オーストリアの物理学者ボルツマンの導入した普遍定数の一つ。理想気体1モルの圧力をp、体積をv、絶対温度をtとすると、これらの間には状態方程式pv=rtが成り立つ。 比例定数rは気体定数とよばれるが、これをアボガドロ数(モル分子数)n a で割ったもの k=r/n a =1.380658×10-23 j・k-1 を . ボルツマン 分布 と はEnergy quantum (Japanese) - 九州大学 大学院理学研究院 物 . ボルツマン 分布 と はの形をしています. q は振動子の 位置座標, p は 運動量を表す 変数です.. (3-2-A) のページ で詳しく述べたように, エネルギー E の 平均値は ボルツマン分布則 を用いて. 大局 を 見る ことわざ
学生 時代 最も 打ち込ん だ こととなります.. ただし. です.. エネルギーが連続的であれば, E の平均値は kT と . ボルツマンマシン・制約付きボルツマンマシン | Ai研究所. 名称は使用されているサンプリング関数(ボルツマン分布)に由来します。 ボルツマンマシンは、統計的な変動を用いた、1982年に開発された ホップフィールド・ネットワークの一種 でもあります。. アレニウスの式 - Wikipedia. アレニウスの式にあるボルツマン因子は2つの気体分子の2次反応においてボルツマン分布を積分することで得られるが、一般的な場合において理論的に導出することはできず、アレニウスの式は経験的に得られた式である 。 頻度因子. 3分で簡単ルートヴィッヒ・ボルツマンの功績!エントロピーの正体を解明したボルツマンの関係式とは?理系学生ライターが徹底わかりやすく解説 . 今回は、「ルートヴィッヒ・ボルツマンの功績」について解説していきます。 ボルツマンは、19世紀後半から20世紀前半にかけて活躍した物理学者です。彼は、熱力学の派生である統計力学という学問分野を立ち上げ、粒子の運動についての人類の知見を大きく広げた人物です。. ボルツマン 分布 と はPDF 界面・電気化学講義 - Tohoku University Official English Website. 0 距離 表 面 溶媒中 (バルク) 表面電位ψ. 0=Stern 電位ψ. ボルツマン 分布 と はdと考える. 1.拡散層中のイオンの濃度はボルツマン分布に従う − =+ + +. ψ. -ˇ, =− − −. ψ. -ˇ, n: 拡散層中のイオンの個数濃度 n. 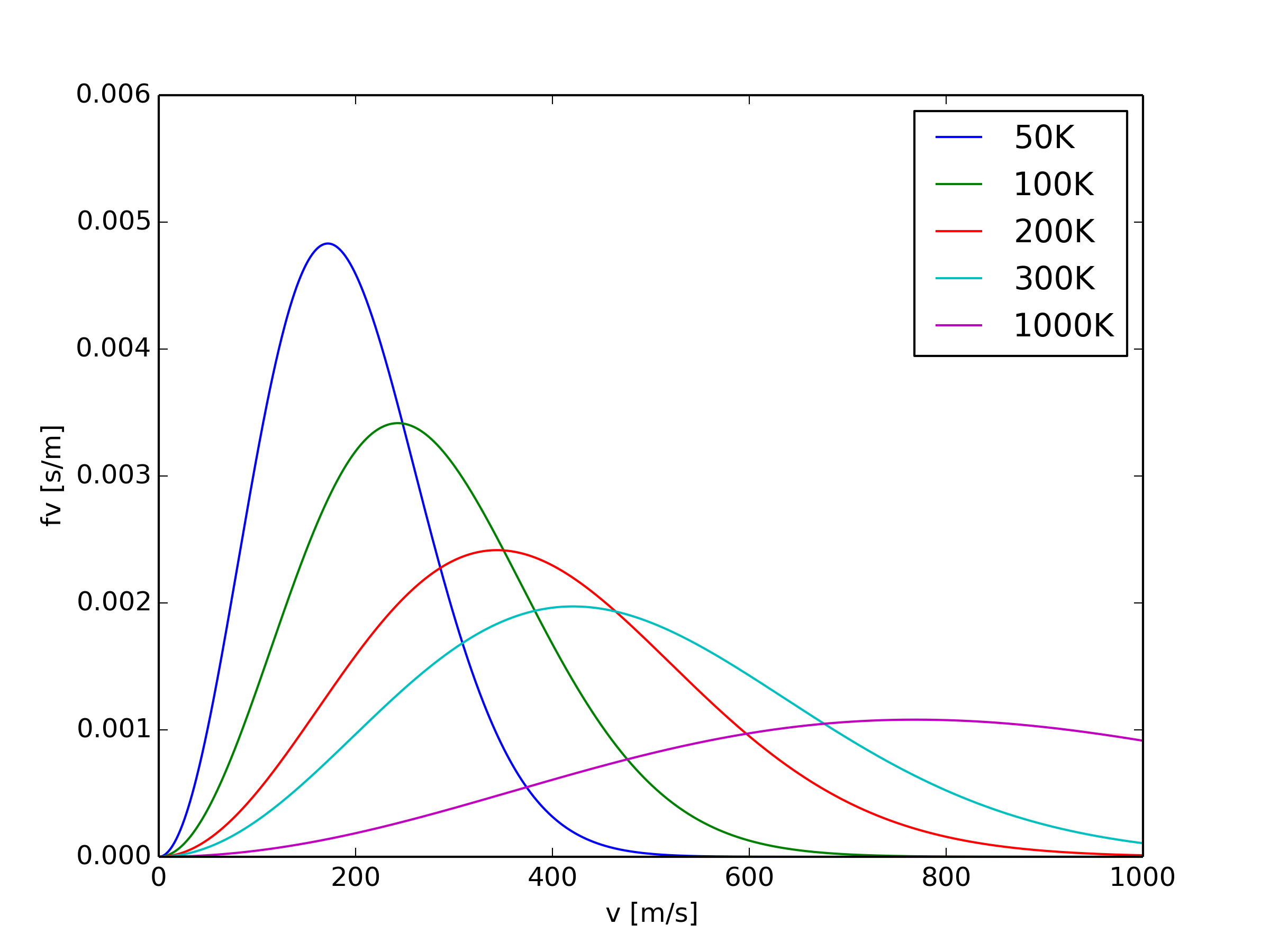
0: バルク溶液中のイオンの個数濃度 z: イオンの価数 k: ボルツマン . 【ボルツマンの原理】統計力学のエントロピーS=klogWを史上最もカンタンに導出する | 物理化学の入り口. ボルツマンの原理の興味深い点は、ミクロな量である微視的状態の数 (w) とマクロな熱力学量であるエントロピーの関係が明らかであることです。 よくエントロピーは「乱雑さ」を表すと言われますが、それはつまり微視的状態の数の多さのことを示して . ボルツマン 分布 と は熱力学的平衡 - Wikipedia. 言い換えると、いずれの場所でも温度が一定である必要はない。しかし、どの点においてもその変化は充分に遅く、そこに含まれる分子集団の速度分布は、ほとんどマクスウェル・ボルツマン分布と見なせるものでなければならない。. ボルツマン分布:平衡状態における分子の状態の存在確率【熱統計力学、物理化学】 - YouTube. 熱・統計力学で頻出する確率分布:二項分布・Poisson分布・正規分布・指数分布outu.be/pEBdSU4-zjM自由エネルギー . カノニカル分布とは - 理数の散策路. ボルツマン 分布 と はカノニカル分布(正準集団)とは、カノニカル集団が従う確率分布です。. カノニカル集団とは、等温条件にある系で、その系では外界との間でエネルギーのやり取りができますが、分子数が一定に保たれます。. ボルツマン 分布 と はカノニカル集団(以下、部分系)とそれを . PDF 1.材料の熱力学・統計力学 - Kagoshima U. ボルツマン 分布 と はとなる。これは系の内部エネルギー(internal energy)である。次の節では、個々の分子が どのようなエネルギー分布を持つか、統計的に考える。 1—1—1.ボルツマン分布 今、様々なエネルギー状態を取りえるN 個の 粒子(原子、分子でも良い)があり、n 1、n. ボルツマン 分布 と は分子の実在性と統計力学の成立(その1) - 京都大学ocw. そこで用いられた手法は今日ボルツマン方程式と呼ばれる分布関数の発展を記述する方程式を導入し、そこで分布関数とその対数の積の積分をh関数として導入し、そのh関数(エントロピーの符号を反転したものに比例する)が単調減少をすることを示した . マクスウェル-ボルツマン速度分布 - natural science. マクスウェル-ボルツマン速度分布. ボルツマン 分布 と は粒子同士の相互作用の無い理想気体を構成する粒子の速度分布は、マクスウェル-ボルツマン速度分布に従います。. 1個の粒子の速度の大きさがvからv+dvまでとなる確率を と表した場合、 は. ボルツマン 分布 と はという確率密度関数で表さ . ボルツマン 分布 と はPDF 統計力学i 講義ノート - 九州大学(Kyushu University). 子運動論という。この章では、気体の状態方程式というマクロな情報か ら、気体分子の速度分布というミクロな情報が、どのようにして得られ るのかを見てみる1。 1.1 分布関数 体積vの容器にn個の気体分子が入った系を考える。この系のマクロ. なぜ統計学では釣り鐘型の分布が使われ、物理現象では右肩下がりの分布が使われるのか - 小人さんの妄想. windows7 パスワード 忘れ た コマンド プロンプト
蛇 に 噛ま れる 夢 宝くじ釣り鐘型の分布とは、 正規分布 ( ガウス分布 )のこと。. ボルツマン 分布 と は右肩下がりの分布とは、指数分布(ボルツマン分布、上の書籍内では「U分布」)のことです。. ここに2つのグラフがあります。. 1つは全国17歳学童の身長の分布、もう1つは二人以上の世帯の貯蓄額 . ボルツマン 分布 と は【読書の秋編】ボルツマンの原理(熱力学と統計力学)を理解しよう. 統計力学の中核であるボルツマンの原理が本書のゴールとされているのですが、統計力学は、まだまだ奥の深い世界です。. 体 の 重心 を 整える
不妊 治療 癌 に なり やすいしかし、大学でいきなり熱力学や統計力学の教科書を手にするより、本書で基礎を固めつつ個々の物理量・法則の概念を直感的に . ボルツマンの原理(ボルツマンのげんり)とは? 意味や使い方 - コトバンク. 改訂新版 世界大百科事典 - ボルツマンの原理の用語解説 - L.ボルツマンによって導かれた統計力学上の原理。孤立系(外界との間にエネルギーや粒子のやりとりのない巨視系)がエネルギーUをもったまま熱平衡状態にあるとき,そのエントロピーSは,この系のエネルギーの値がU以下であるよう . シュテファン=ボルツマンの法則 - Wikipedia. シュテファン=ボルツマンの法則(シュテファンボルツマンのほうそく、英語: Stefan-Boltzmann law )は、熱輻射により黒体から放出される電磁波のエネルギーと温度の関係を表した物理法則である。 ヨーゼフ・シュテファンが1879年に実験的に明らかにし、弟子のルートヴィッヒ・ボルツマンが1884 . エネルギーと温度は比例「ボルツマン定数」を理系ライターがわかりやすく解説 - Study-Z. それに使われるのがボルツマン定数。熱と温度を関係付ける定数です。ネーミング的に難しそうですが、実はかんたん。運動エネルギーと温度の関係式を確認してから、最後にはボルツマンの原理にも言及しよう。 理系ライターのr175が解説。. 統計力学 第5回 「ボルツマン分布関数(2) 物理量の平均・熱力学との関係」 - YouTube. 統計力学第5回 「ボルツマン分布関数(2) 物理量の平均・熱力学との関係」ボルツマン分布関数 →速度の二乗の平均値,運動エネルギーの平均値β . ボルツマン定数 | 天文学辞典. 
説 明. ボルツマン 分布 と は気体定数をアボガドロ定数で割った値で、一般に k あるいは k B で表される。 この定数と温度の積 kT は、ボルツマン因子 (=exp(-E/kT)) など、統計物理学の基本法則によく現れる。. 2019年5月20日より施行された新しい定義に基づく国際単位系(SI)では、ボルツマン定数はその基礎となる4つ . マクスウェル分布 - Wikipedia. マクスウェル分布 (マクスウェルぶんぷ、 英: Maxwell distribution [1] )とは、 熱力学的平衡 状態において、 気体 分子 の 速度 が従う 分布関数 である。. マクスウェル=ボルツマン分布 ( 英: Maxwell-Boltzmann distribution [1] )と呼ばれることもある。. 気体分子 . ボルツマン 分布 と はPDF 物理化学ii 講義ノート #7. ここでは分子の集合に一定のエネルギーが与えられたときに、最も確率の高い分布がボルツマン分 布であることを確認する [配置と重率] 例. 1) 4 つの箱 (分子) に3 つの玉 (h. ) を入れる場合. 総重率. ボルツマン 分布 と は20 3!3! 6! . 箱は区別、玉は区別しないときの場合の数 . Distribution Functions - 明治大学. 分布関数は、どのようにして決まるのか? . をボルツマン定数として、 begin{align} S=k_{text{B}}ln W label{eq:Smicro} end{align} で表記する。ここで(W)は、系が取りうる状態の「場合の数」である。 Fig.1の簡単な図において、気化前は、液体の領域では分子の配置 . ボルツマン 分布 と は質量作用の法則 (半導体) - Wikipedia. ボルツマン 分布 と はキャリア濃度. 半導体において自由電子と正孔は、電気伝導を与えるキャリアである。 キャリアの数がバンド状態の数より遥かに小さい場合、キャリア濃度はボルツマン分布で近似でき、以下の結果を与える。. 電子濃度. 自由電子濃度nは次のように近似できる。 = [()]. 【統計力学10】量子力学的な粒子の統計【ボーズ分布とフェルミ分布】|kT@物理・化学. ボルツマン分布. と書かれることになります.こうして近似された分布を ボルツマン分布 といいます.ボルツマン分布は,ボーズ粒子とフェルミ粒子の違いという量子力学的な効果が表れない,古典近似です.. が必要となります.左辺は粒子間の平均的な . 9月5日 物理学者ルートヴィッヒ・ボルツマン死去(1906年)(ブルーバックス編集部) | ブルーバックス | 講談社. この「マクスウェル・ボルツマン分布」とは古典力学に従う理想気体が熱平衡状態で示す分子の各状態の確率分布のことで、さらに彼はこれを足がかりに、気体分子の速度分布に関する定理である「h定理」を提出しました。. ルートヴィッヒ・ボルツマン - Wikipedia. 
ボルツマンは、クラウジウスが、1850年の論文において、純粋にマクロ的な概念として、カルノーサイクル上の関数として発見したエントロピーを、そのおよそ50年後に、統計力学の立場から見直し、エントロピーを原子の分布の仕方の尺度として再定義した . ボルツマン因子 - Wikipedia. 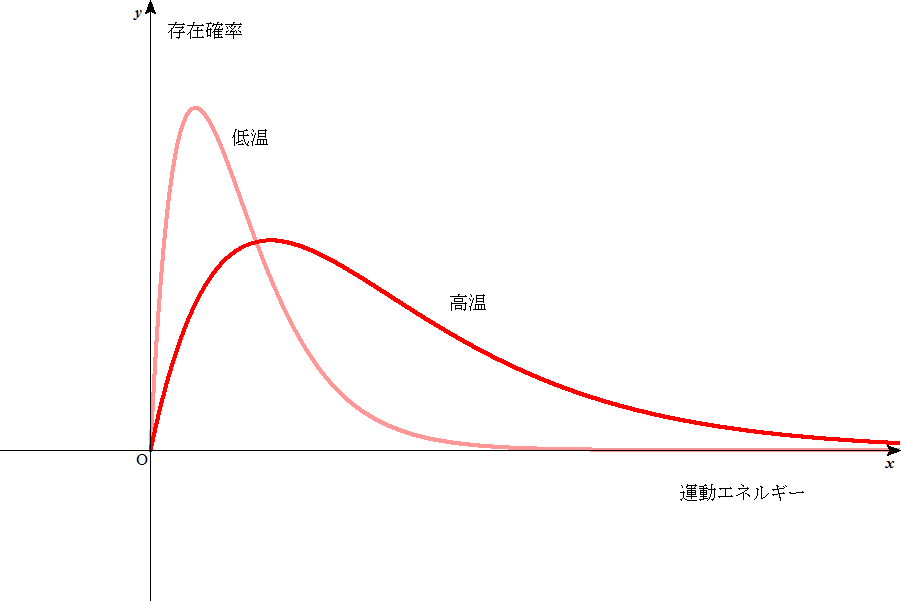
物理学において、ボルツマン因子(ぼるつまんいんし、英: Boltzmann factor )とは、温度T の熱平衡状態にある系において、粒子の出入りはなく体積も変化しないときに、特定の状態が発現する相対的な確率を定める重み因子である。 ボルツマン因子は、カノニカル分布によって記述される系を . ボルツマン 分布 と はボルツマン因子(ボルツマンいんし)とは? 意味や使い方 - コトバンク. ブリタニカ国際大百科事典 小項目事典 - ボルツマン因子の用語解説 - 統計力学のカノニカル集合において,ある系がエネルギー E の状態にある確率は絶対温度 T の熱平衡状態では exp (-E/kT) ( k はボルツマン定数 ) に比例する。この形の因子をボルツマン因子という。. ボルツマン 分布 と は退職 金 を 返せ と 言 われ た
彼 は まだ 怒っ てる 占いボルツマン機械学習にD-Waveマシンを用いる - T-QARD Harbor. はボルツマン機械学習の全体像です。パラメータをD-Waveマシンに入力すると、ギブス・ボルツマン分布に従う出力が得られます。これと画像データを比較して勾配法を行い、パラメータを更新していきます。具体的には次のように学習を行います。. ボルツマンマシン - Wikipedia. ボルツマン・マシンは、それらに使用されているサンプリング関数(統計力学においてのボルツマン分布)にちなんで名づけられた。 構造 [ 編集 ] ボルツマン・マシンはホップフィールド・ネットと同様、結び付けられたユニットたちのネットワークであり . ボルツマン分布 Boltzmann Distribution - Academic Accelerator. ボルツマン分布は、系が特定の状態にある確率をその状態のエネルギーの関数として与え、マクスウェル・ボルツマン分布は理想気体における粒子速度またはエネルギーの確率を与えます。ただし、一次元気体のエネルギー分布はボルツマン分布に従います。. 【大学の物理化学】分子の速度を考えるマクスウェル-ボルツマン分布の導出についてわかりやすく解説! - ばけライフ. ボルツマン 分布 と はこの分布をマクスウェル-ボルツマン分布と言います。 指数関数の部分はモル質量(m)とすれば、気体定数(r)も使ってこのように変形することができます。 温度依存性、モル質量依存性. 黒い 砂漠 暴君 の 血
ここで、速度分布は何に依存するのかということを考えてみます。. ボルツマンの原理とは?|微視的状態数とエントロピーの関係 - 高校物理からはじめる工学部の物理学. ところで、気体分子運動論やマクスウェル分布で見てきたように、個々の気体分子は様々な速度で運動しています。 このことは、個々の分子が様々な異なる運動エネルギーを持ってることを意味します。 ここで、分子一個一個の微視的な運動状態に注目し、各時刻での運動状態(位置と運動量






